how to find the distance between two parallel lines

Altitude between 2 parallel lines is the perpendicular distance from any indicate to one of the lines. In this article, you will learn parallel lines definition, how to detect the distance between them, and solved examples.

The graph of the part, a pair of railroad tracks, or the opposite sides of a parallelogram or keys of a piano can be a few examples of parallel lines. A mutual property that can be institute in the in a higher place examples is that the two railroad tracks never meet, the opposite sides of a parallelogram volition never intersect or the piano keys are parallel to each other. This article explains the method of finding the distance between ii parallel lines with appropriate examples.

Parallel Lines Definition

Parallel lines are those lines that never meet each other. When the distance between a pair of lines is the same throughout, information technology tin exist called parallel lines. It is denoted past "||". The chief criteria for any two lines to be parallel is that they have to be fatigued on the same aeroplane. They are ever equidistant from each other.

The lines can be extended till infinity. The slopes of two parallel lines are equal.

How to Find the Altitude Between Two Parallel Lines

The method for computing the distance between ii parallel lines is as follows:

• Ensure whether the equations of the given parallel lines are in slope-intercept course (y=mx+c).
• The intercepts (c_i and c_two) and gradient value which is common for both the lines has to exist determined.
• Afterward obtaining the above values, substitute them in the slope-intercept equation to notice y.
• Finally, put all the above values in the altitude formula to find the distance between two parallel lines.

The two parallel lines can exist taken in the form

y = mx + c_one … (i)

and y = mx + c_ii … (two)

The line (2) will intersect the x-axis at point A (–c₁/m, 0) as shown in the figure.

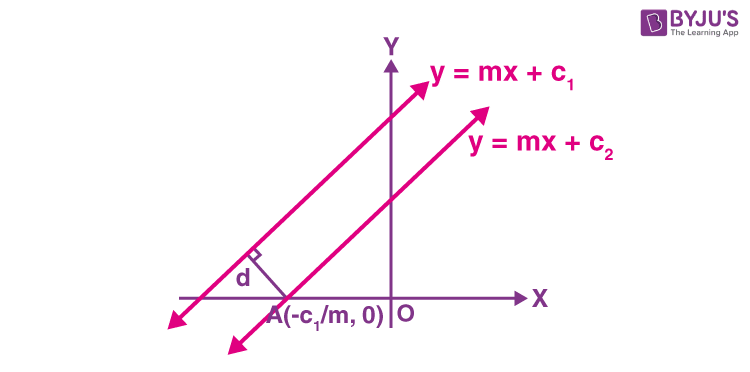
The length of the perpendicular from indicate A to the line (i) is of the same length every bit the distance between two lines.

Therefore, the altitude between the lines (i) and (ii) is

|(–m)(–c₁/thousand) + (–c_two)|/√(ane + g²) or d = |c₁–c₂|/√(1+m^two).

Altitude d between two parallel lines y = mx + c₁ and y = mx + c_ii is given past

d = |C₁–C₂|/√(A² + B^two)

Altitude betwixt a point (x₁, y₁) and a line is d= |a_anex_ane+b_oney_ane+c_ane| / √(a₁ ^two +b ₁ ² ) ,

where a ₁ and b_one are the coefficients of variable x and y in the equation of the line.

The equation of line is

a_anex+b_iy+c_i = 0

Considering the following equations of 2 parallel lines, we tin can calculate the altitude between those lines using the distance formula

ax+by+c = 0

ax+past+c₁ = 0

Using the above ii equations nosotros can conclude that

Distance betwixt ii parallel lines, d = |c-c₁| / √(a ² +b ² )

Also read

Height and distance bug

Trigonometric equations

Solved Examples

Case 1: Observe the distance of the bespeak (four, –half-dozen) from the line 2x – 7y – 24 = 0.

Solution:

Given line is 2x – 7y – 24 = 0. …… (1)

Comparing (1) with general equation of line Ax + By + C = 0, nosotros get

A = 2, B = –7 and C = –24.

Given point is (x_i, y₁) = (iv, –half dozen).

The distance of the given point from given line is d = |Ax_ane + Past_ane + C|/√Aⁱⁱ+B² = 26/seven.two

= 3.6

Case 2: Judge the altitude between the two parallel lines y=2x+7 and y=2x+5.

Solution:

The distance between two parallel lines is given by |c₁-c₂|/√(a ² +b ^two ).

Hither, the equations of parallel lines are y = 2x + 7 and y = 2x + 5.

Slopes are same m_ane = m_ii = 2 and c₁ = vii ,c₂ = 5.

here a = 2, b = -1

So, the distance between ii parallel lines is given by

=> |c₁-c₂| = |vii-v|/√(2 ² +1 ² ) = ii/√v

Example 3: Calculate the distance between the parallel lines 3x+4y+seven=0 and 3x+4y−five=0 .

Solution:

The distance between two parallel lines is given by d = |c_ane-c₂|/√(a ² +b ² ).

Here c₁= 7, c_two = -5, a = 3, b = iv

so d = |7 – (-5)|/√(iii ^two +4 ⁱⁱ )

= 12/5

Example 4: Find the distance from the line 6x – 4y + 36 = 0 to point (0, 0).

Solution:

Distance betwixt a signal (x₁, y₁) and a line a_i10+b₁y+c₁ = 0 is

d = |a_iten₁+b₁y₁+c₁| / √(a_i ² +b _one ⁱⁱ )

Hither a₁ = 6, b_ane = -4, c_i = 36,x_i = 0, y₁ = 0

so d = 36/√(36 + xvi)

= 36/√52

Example 5: Let PS be the median of the triangle with vertices

\(\begin{array}{fifty}P(2,\ 2),\ Q(6,\ -\ 1)\end{assortment} \)

and

\(\begin{array}{l}R(7,\ iii)\stop{array} \)

. The equation of the line passing through (ane, -1) and parallel to PS is

A) 2x − 9y − 7 = 0

B) 2x − 9y − xi = 0

C) 2x + 9y − 11 = 0

D) 2x + 9y + vii = 0

Solution:

S = midpoint of

\(\begin{array}{fifty}QR=\left( \frac{half-dozen+7}{2},\,\frac{-1+3}{two} \correct)=\left( \frac{13}{2},\,1 \right)\\\terminate{array} \)

Slope of

\(\begin{assortment}{l}PS=\frac{2-one}{ii-\frac{thirteen}{2}}=-\frac{2}{9}\\\terminate{array} \)

Equation of line passing through (10_i, y₁) having slope m is y – y₁ = m(10 – 10₁)

The required equation is

\(\begin{array}{fifty}y+1=\frac{-two}{9}(ten-i)\stop{assortment} \)

that is

\(\begin{assortment}{fifty}2x+9y+7=0.\end{array} \)

.

Instance 6:The graph of the function

\(\begin{array}{l}\cos 10\ \cos (x+2)-{{\cos }^{ii}}(x+one)\end{assortment} \)

 is

A) A direct line passing through (0,−sin² one) with slope 0

B) A straight line passing through (0, 0)

C) A parabola with vertex 75 degrees

D) A straight line passing through the point (π/ 2, −sin² 1) and parallel to the ten-axis

Solution:

\(\begin{array}{l}y=\cos (x+1-i)\cos (ten+1+1)-{{\cos }^{2}}(ten+1) \\={{\cos }^{2}}(x+i)-{{\sin }^{2}}1-{{\cos }^{two}}(x+1)=-{{\sin }^{2}}1,\\\cease{array} \)

 which represents a direct line parallel to x-axis, it passes through  (0, −sin^two i).

Here slope = 0

Hence choice A is the answer.

Example 7:The line 3x + 2y = 24 meets y-axis at A and x-axis at B. The perpendicular bisector of AB meets the line through (0,−one) parallel to the ten-axis at C. The area of the triangle ABC is

A) 182sq.units

B) 91sq.units

C) 48sq.units

D) None of these

Solution:

The coordinates of A and B are (0, 12) and (8, 0) respectively.

Slope of given line  3x + 2y = 24 is m = -three/2

Gradient of perpendicular bisector = two/three

Midpoint of AB = (4, 6)

The equation of the perpendicular bisector of AB is

\(\brainstorm{array}{fifty}y-6=\frac{ii}{3}(10-4) \text \ or \ 2x-3y+10=0 …..(i)\\\end{array} \)

Equation of a line passing through (0, one) and parallel to the x-centrality is y=−1.

(substitute y = -1 in 2x-3y+10=0)

This meets (i) at C, Therefore the coordinates of C are

\(\begin{array}{fifty}\left( -\frac{13}{2},-1 \correct)\end{array} \)

.

Hence, the area of the triangle ABC is

\(\begin{array}{l}\Delta =\frac{one}{ii}\left| \brainstorm{matrix} 0 & 12 & i \\ eight & 0 & 1 \\ -\frac{13}{2} & -1 & ane \\ \finish{matrix}\, \right|=91 \text \ sq. \ units.\stop{array} \)

Example eight: The diagonals of a parallelogram PQRS are along the lines x + 3y = 4 and 6x − 2y = 7. Then PQRS must be a

A) Rectangle

B) Square

C) Cyclic quadrilateral

D) Rhombus

Solution:

Given 10 + 3y = 4  ..(i)

6x − 2y = 7  ..(ii)

g_one = −one/3 and yard₂ = iii.

here yard₁m_two = -ane

Hence, lines x + 3y = 4 and 6x − 2y = 7 are perpendicular to each other.

Therefore, the parallelogram is a rhombus.

Case ix:

Find the distance between the lines  4x +3y+vi= 0 and  4x+3y-3= 0.

Solution:

Here A = 4, B = three,  C1 = half-dozen and C2 = -three

So the distance =| (C1-C2) | / √(A²+B^two)

=| (vi–3) |  / √(16+9) = ix/√25 = 9/5

Source: https://byjus.com/jee/distance-between-2-parallel-lines/#:~:text=The%20distance%20between%20two%20parallel%20lines%20is%20given%20by%20d,a2%2Bb2).&text=Example%204%3A%20Find%20the%20distance,point%20(0%2C%200).

Posted by: hiebertclould.blogspot.com

Share this post