can you find the square root of a negative number

Let'southward investigate what happens when negative values appear under the radical symbol (equally the radicand) for cube roots and square roots.

In some situations, negative numbers under a radical symbol are OK. For example, is not a problem since (-2) • (-2) • (-2) = -8, making the respond -ii. In cube root problems, it is possible to multiply a negative value times itself three times and get a negative reply.

Difficulties, however, develop when we look at a problem such as . This foursquare root problem is request for a number multiplied times itself that will requite a product (answer) of -16. There simply is no way to multiply a number times itself and become a negative result. Consider: (4) • (four) = sixteen and (-4) • (-four) = 16.

CUBE ROOTS:	BUT	SQUARE ROOTS:
Yep, (-ii) ten (-2) ten (-2) = -eight. No problem.		Nope! (4) x (4) ≠ -16. Nope! (-four) 10 (-4) ≠ -16.

Square roots are the culprits! The difficulties arise when you see a negative value nether a square root. It is non possible to square a value (multiply it times itself) and arrive at a negative value. And so, what exercise we exercise?

The square root of a negative number does not exist among the set up of Real Numbers.

When problems with negatives under a foursquare root first appeared, mathematicians thought that a solution did not exist. They saw equations such every bit x ² + 1 = 0 , and wondered what the solution really meant.

In an effort to address this problem, mathematicians "created" a new number,

i , which was referred to as an "imaginary number" , since it was not in the set of "Real Numbers". This new number was viewed with much skepticism. The imaginary number first appeared in impress in the year 1545.

The imaginary number "i" is the foursquare root of negative one.

An imaginary number possesses the unique property that when squared, the issue is negative.

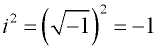
irad1

Consider:
The process of simplifying a radical containing a negative gene is the same as normal radical simplification. The only deviation is that the will be replaced with an " i ".

Equally research with imaginary numbers continued, it was discovered that they really filled a gap in mathematics and served a useful purpose. Imaginary numbers are essential to the study of sciences such as electricity, quantum mechanics, vibration analysis, and cartography.

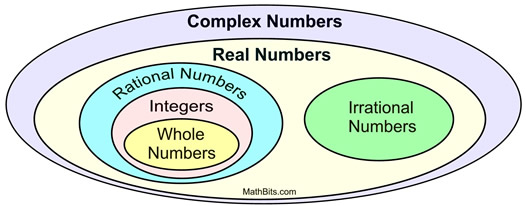
When the imaginary i was combined with the set of Real Numbers, the all encompassing set of Complex Numbers was formed.

complex

Production Rule

where a ≥ 0, b≥ 0

"The foursquare root of a product is equal to the product of the square roots of each factor."

This theorem allows us to use our method of simplifying radicals.

Imaginary (Unit) Number

Production Dominion
(extended) where a ≥ 0, b≥ 0
OR a ≥ 0, b < 0
but
Not a < 0, b < 0

FYI: The powers of i e'er cycle through just four dissimilar values:
i ¹ = i
i ² = -1
i ³ = -i
i ⁴ = i
i ⁵ = i and the cycle starts again.

When doing arithmetics on i , care for it equally yous would an "ten".
3 i + 4 i = 7 i
2 i • 4 i = 8 i ² = -8
Note: i ² was replaced with -1.

Do NOT confuse "irrational" numbers
with
"imaginary" numbers.
They are Not the same.

Complex Numbers
a ± bi
where a and b are real numbers, and i is the imaginary unit of measurement.

Complex numbers are written in the standard grade a + bi.

In Algebra 1, you will see that the "imaginary" number will exist useful when solving quadratic equations. The quadratic formula may requite complex solutions, written as a ± bi, where a and b are real numbers.
You will see more than about imaginary numbers in the Quadratic section.

Source: https://mathbitsnotebook.com/Algebra1/Radicals/RADNegativeUnder.html

Posted by: hiebertclould.blogspot.com